[题解] [Mivik Round nurture] Something Comforting

给出 一个生成括号序列的算法 和一个长度为 $2n$ 的合法括号序列，问这个括号序列通过这种算法被生成的概率。答案对 $998244353$ 取模。

$1\le n\le 5\cdot 10^5$

题目链接

---

思路

我们还是把括号序列转换成那个经典的“走右上右下”的形式，即从 $(0,0)$ 开始行走，左括号是向右上走，右括号是向右下走，那么一个括号序列合法等价与行走轨迹不越过 X 轴。比如下图是 ()(()) 对应的行走轨迹：

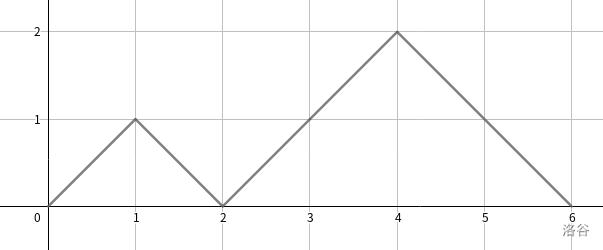
我们发现，算法最开始随机 random_shuffle 出来的括号序列，对应着一个可能越过了 X 轴，但最终走到了 $(2n,0)$ 的行走轨迹（因为左括号右括号数目相等）。然后仔细观察我们的算法，实际上就是找到第一个低于 X 轴的位置和在这个位置后第一次走回 X 轴的位置，并把中间的一段翻到 X 轴上去了。这样必定能形成最终的合法括号序列。

于是答案就显而易见了。由于在翻转过程中我们的行走轨迹中与 X 轴相交的那些点是不变的，所以如果一个合法的括号序列对应的行走轨迹有 $m$ 个点与 X 轴相交，它就可能由 $2^{m-1}$ 次方种括号序列得到（每一个部分在 X 轴上方或者下方），所以答案就是 $\frac{2^{m-1}}{\binom{2n}n}$。

代码

mivik.h

代码